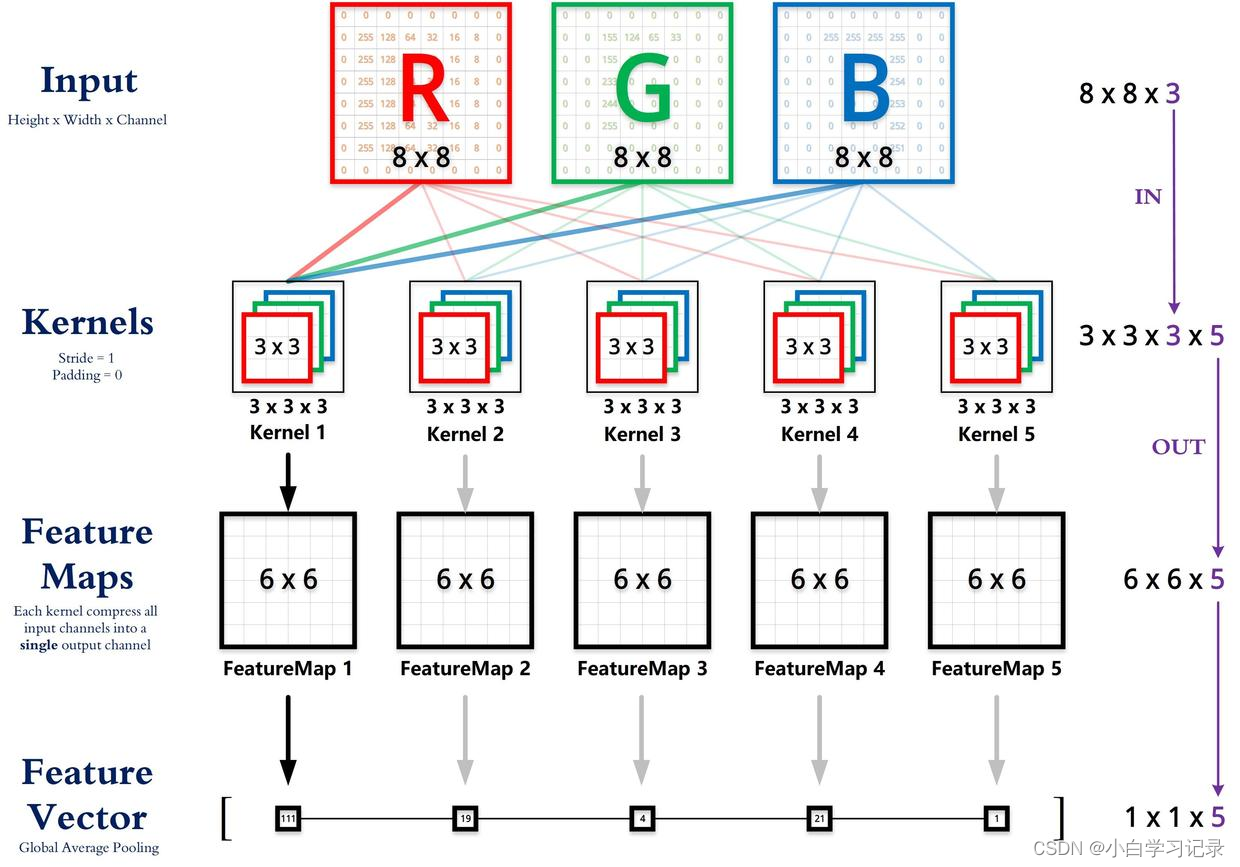
卷积层尺寸的计算原理
输入矩阵格式:四个维度,依次为:样本数、图像高度、图像宽度、图像通道数
输出矩阵格式:与输出矩阵的维度顺序和含义相同,但是后三个维度(图像高度、图像宽度、图像通道数)的尺寸发生变化。
权重矩阵(卷积核)格式:同样是四个维度,但维度的含义与上面两者都不同,为:卷积核高度、卷积核宽度、输入通道数、输出通道数(卷积核个数)
输入矩阵、权重矩阵、输出矩阵这三者之间的相互决定关系
卷积核的输入通道数(in depth)由输入矩阵的通道数所决定。(红色标注)
输出矩阵的通道数(out depth)由卷积核的输出通道数所决定。(绿色标注)
输出矩阵的高度和宽度(height, width)这两个维度的尺寸由输入矩阵、卷积核、扫描方式所共同决定。计算公式如下。(蓝色标注)
卷积后输出图片大小:N = (W-F+2P)/ S +1
W:输入图片,F:卷积核尺寸,S:步长, P: 填充
标准卷积计算举例
以 AlexNet 模型的第一个卷积层为例,
输入图片的尺寸统一为 227 x 227 x 3 (高度 x 宽度 x 颜色通道数),
本层一共具有96个卷积核,
每个卷积核的尺寸都是 11 x 11 x 3。
已知 stride = 4, padding = 0,
假设 batch_size = 256,
则输出矩阵的高度/宽度为 (227 - 11) / 4 + 1 = 55
1 x 1 卷积计算举例
后期 GoogLeNet、ResNet 等经典模型中普遍使用一个像素大小的卷积核作为降低参数复杂度的手段。
从下面的运算可以看到,其实 1 x 1 卷积没有什么神秘的,其作用就是将输入矩阵的通道数量缩减后输出(512 降为 32),并保持它在宽度和高度维度上的尺寸(227 x 227)。
- 原理是什么?卷积核的个数决定了输出的特征图的个数,也就是特征图的通道数,或者说是卷积后的输出的通道数,因此可以使用远小于原来的输入特征图通道数个1×1卷积核来压缩通道数。

全连接层计算举例
实际上,全连接层也可以被视为是一种极端情况的卷积层,其卷积核尺寸就是输入矩阵尺寸,因此输出矩阵的高度和宽度尺寸都是1。
总结:
其实只需要认识到,虽然输入的每一张图像本身具有三个维度,但是对于卷积核来讲依然只是一个一维向量。
- 卷积核做的,其实就是与感受野范围内的像素点进行点积(而不是矩阵乘法)。
- 输入 x:[batch, height, width, in_channel]
- 权重 w:[height, width, in_channel, out_channel]
- 输出 y:[batch, height, width, out_channel]
相关代码使用
**1 torch.nn.LSTM() **
torch.nn.LSTM(input_size,hidden_size,num_layers,bias=True,batch_first=False)input_size: 输入数据的特征维数,通常就是embedding_dim(词向量的维度)
hidden_size :LSTM中隐层的维度
num_layers :循环神经网络的层数
bias :用不用偏置,default=True
batch_first :如果是True,则input为(batch, seq, input_size)【batch大小,序列长度,特征数目】。默认值为:False(seq_len, batch, input_size)
dropout: 默认是0,代表不用dropout
bidirectional:默认是false,代表不用双向LSTM
2 torch.nn.Conv2d()
参数dilation——扩张卷积(也叫空洞卷积)
扩张操作(dilation):控制kernel点(卷积核点)的间距,默认值:1。
dilation操作动图演示如下:
Dilated Convolution with a 3 x 3 kernel and dilation rate 2
扩张卷积核为3×3,扩张率为2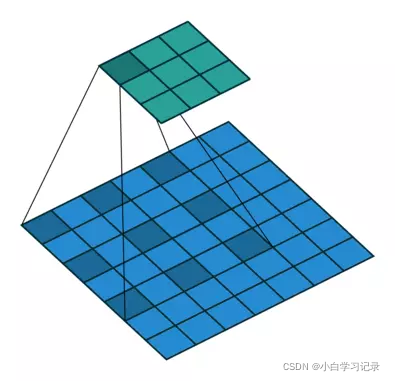
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)3 torch.nn.MaxPool2d()
torch.nn.MaxPool2d(kernel_size,stride,padding=0,ceil_mode=False)kernel_size :表示做最大池化的窗口大小,可以是单个值,也可以是tuple元组(例如3->(3,3),或者(2,3))
stride :步长,可以是单个值,也可以是tuple元组
默认步长跟最大池化窗口大小一致。
padding :填充,可以是单个值,也可以是tuple元组
dilation :控制窗口中元素步幅
return_indices :布尔类型,返回最大值位置索引
ceil_mode :布尔类型,为True,用向上取整的方法,计算输出形状;默认是向下取整。
4 torch.nn.Linear()
torch.nn.Linear(in_features,out_features,bias=True)in_features: 上层神经元个数【每个输入样本的大小】
2)out_features: 本层神经元个数【每个输出样本的大小】
3)bias: 偏置,形状[out_features]。网络层是否有偏置,默认存在,且维度为[out_features ];若bias=False,则该网络层无偏置,图层不会学习附加偏差
5 torch.nn.Dropout(0.1)
设置 Dropout 时,torch.nn.Dropout(0.9), 参数表示要丢弃的比例,这里的 0.1 是指该层(layer)的神经元在每次迭代训练时会随机有 10% 的可能性被丢弃
6 batch_normalization 1D
可以使用batch_normalization对隐藏层的数据进行正态分布标准化,由于标准化后可能影响神经网络的表达能力。 normalize 后的数据再使用缩放系数γ和平移系数β进行缩放和平移。其中γ和 β参数需要进行进行反向传播学习,使得处理后的数据达到最佳的使用效果。
torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)BatchNorm1d接收一个二维的输入with维度(batch_size,num_features)。
num_features:通道数
momentum: 计算running_mean和running_var的滑动平均系数。采用下列的公式
affine:bool值,True表示使用γ和 β参数
track_running_stats:bool值,如果为True,训练阶段采用实时的batch均值和方差, 同时采用滑动平均来计算全局的running_mean和running_var,测试阶段采用当前的running_mean和running_var;如果是False,则训练阶段和测试阶段都采用实时的batch均值和方差。
好处:
(1)BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度
BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内,使得后一层网络不必不断去适应底层网络中输入的变化,从而实现了网络中层与层之间的解耦,更加有利于优化的过程,提高整个神经网络的学习速度。
(2)BN使得模型对初始化方法和网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定
(3)BN允许网络使用饱和性激活函数(例如sigmoid,tanh等),缓解梯度消失问题
7 torch.optim.Adam
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
参数:
- params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
- lr (float, 可选) – 学习率(默认:1e-3)
- betas (Tuple[float, float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999),betas = (beta1,beta2)
beta1:一阶矩估计的指数衰减率(如 0.9)。
beta2:二阶矩估计的指数衰减率(如 0.999)。 - eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8),epsilon:该参数是非常小的数,其为了防止在实现中除以零(如 10E-8)。
- weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0),选择0.01比较好
代码
# CNN
# 0、导入工具包
import torch.utils.data as Data #导入data数据集
from torch.autograd import Variable
import torch.nn as nn
import torch
import torch.optim
import data_load
import numpy as np
# 1、载入数据集
train_x,train_y,_,_=data_load.data_load1_FFT()
_,_,test_x,test_y=data_load.data_load3_FFT()
[m,n]=np.shape(train_x)
[m_test,_]=np.shape(test_x)
print(train_x.shape)
# 2、设置超参数
EPOCH = 500
BATCH_SIZE = 20
LR = 4e-6
# 3、DataLoader获取迭代数据
train_x=torch.from_numpy(train_x.reshape([m,1,n])).float()
train_y=torch.from_numpy(train_y).float()
test_x=torch.from_numpy(test_x.reshape([m_test,1,n])).float()
test_y=torch.from_numpy(test_y).float()
## TensorDataset-用于tensor打包,类似zip功能
train_set = Data.TensorDataset(train_x,train_y)
## 定义迭代器,获取迭代数据
train_loader=Data.DataLoader(dataset=train_set,batch_size=BATCH_SIZE,shuffle=False)
# 4、定义模型
class Model(nn.Module):
def __init__(self):
super(Model,self).__init__()
self.layer1=nn.Sequential(
nn.Conv1d(1,8,5),
nn.ReLU(),
nn.MaxPool1d(5))#输出为[50,100,24]
self.layer2=nn.Sequential(
nn.Conv1d(8,16,3),
nn.ReLU(),
nn.MaxPool1d(3))
self.fc=nn.Sequential(nn.Linear(400,250),nn.ReLU(),
nn.Linear(250,150),nn.ReLU(),
nn.Linear(150,80),nn.ReLU(),
nn.Linear(80,30),nn.ReLU(),
)
self.fc2=nn.Sequential(nn.Linear(30,7),nn.Softmax(dim=1))
def forward(self,x):
out=self.layer1(x)
out=self.layer2(out)
out=out.view(out.size(0),-1)
# print(out.size())#显示当前输出的维度
out=self.fc(out)
out=self.fc2(out)
return out
# 5、模型实例化,定义优化器、损失函数
model=Model()
print(model)
optimizer = torch.optim.Adam(model.parameters(), lr=LR)#定义优化器
loss_function =nn.CrossEntropyLoss()#定义损失函数
# 6、训练模型
for epoch in range(EPOCH):
model.train() # 在训练模型时会在前面加上:
for step, (x, y) in enumerate(train_loader):
batch_x = Variable(x)
batch_y = Variable(y)
batch_x=batch_x.float()
output = model(batch_x) # 输入训练数据
loss = loss_function(output, batch_y.long()) # 计算误差
optimizer.zero_grad() # 清空上一次梯度
loss.backward() # 误差反向传递
optimizer.step() # 优化器参数更新
model.eval() # 在测试模型时会在前面加上:
if epoch%10 == 0:
test_output=model(test_x)
pred_y=torch.max(test_output,1)[1].numpy()
accuracy=(pred_y==test_y.numpy()).mean()
# accuracy=sum(pred_y==test_y.numpy())/test_y.size(0)
print('Epoch:',epoch,'|Step:',step,'|train loss:%.4f'%loss.data.numpy(),
'|test accuracy:%.4f'%accuracy)
